|
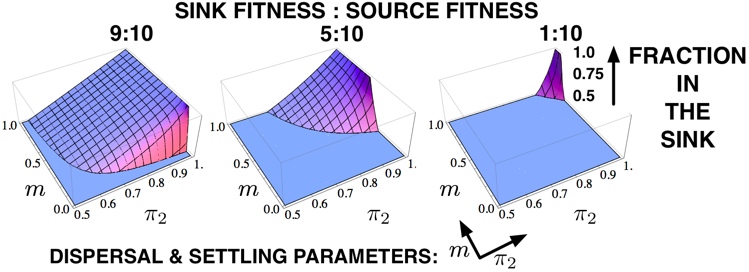
| Fraction of stationary population in the sink habitat as a function of dispersal rate m and sink settlement rate π2 in the Deakin model. Only sink fractions that are 50% and above are plotted. Census is just before dispersal. |
Dedicated to the memory of Prof. Michael ‘Miki’ Neumann, one of whose many elegant theorems provides for a result presented here.
Ecological Monographs 83(3): 297-333. Submitted, June 2011.

|
| Fraction of stationary population in the sink habitat as a function of dispersal rate m and sink settlement rate π2 in the Deakin model. Only sink fractions that are 50% and above are plotted. Census is just before dispersal. |
McNamara and Dall (2011) identified novel relationships between 1) the abundance of a species in different environments, 2) the temporal properties of environmental change, and 3) selection for or against dispersal. Here, the mathematics underlying these relationships in their two-environment model are investigated for arbitrary numbers of environments. A population statistic, the fitness-abundance covariance, is introduced, which quantifies the property they describe. It is the covariance between growth rates and the excess abundance of the population over what it would be without heterogeneous growth rates. Its value depends on the phase in the life cycle when the population is censused, and the pre-dispersal and post-dispersal values differ as an example of Fisher’s Fundamental Theorem. The post-dispersal values are shown to connect with the Reduction Principle from the population genetics literature on the evolution of genetic systems and migration, which is reviewed. Conditions that produce selection for increased unconditional dispersal are new instances of the ‘Principle of Partial Control’ proposed to explain departures from reduction in the evolution of modifier genes. According to this principle, variation that only partially controls the processes that transform the transmitted information of organisms may be selected to increase these processes. Mathematical methods of Karlin, Friedland, and Elsner, Johnson, and Neumann, are central in generalizing the analysis. The model’s behavior is shown to depend on the harmonic mean of the durations of the environments, and the eigenvalues of the environmental change matrix. Analysis of the adaptive landscape in the model shows that the evolution of conditional dispersal is very sensitive to the spectrum of phenotypic variation produced by the population, and suggests that empirical study of a particular species will require an evaluation of its variational properties.
Keywords: migration modifier, reversible Markov chain, source-sink, ideal free distribution, ESS, invasibility, balanced dispersal, directed mutation, evolution of traditionalism, spatial heterogeneity, length of runs, stationary distribution
|
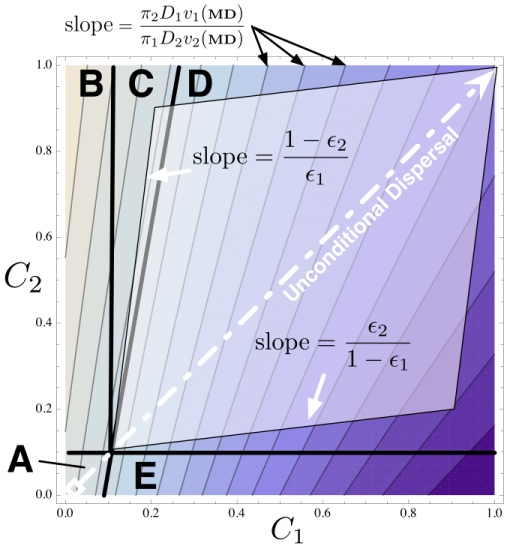
| The adaptive landscape for conditional dispersal in the model of McNamara and Dall (2011). Gradient shows the asymptotic growth rate of the population as a function of conditional dispersal rates C1 and C2. |
This is a very important paper that shows how many studies in the theories of evolution and evolutionary ecology can be unified under a general mathematical framework. The work is deep and the mathematics heavy-going. Nevertheless I recommend urgent acceptance of the paper because of the great importance and generality of the work. |
I really liked the formal connections that the author was able to demonstrate with previous work on mutation rates, recombination and cultural dynamics. This analysis will go a long way to advancing a general theory of eco-evolutionary dynamics that is being pursued more and more in the literature nowadays. I look forward to spending time meditating further on this work (and the other theory this work draws upon) to enhance my understanding of information dynamics in evolved systems. ... On the whole, for such a technical work, it is very clearly written and the arguments are well-explained throughout. |
This is an important synthetic work, and the reviewers and I appreciate the work you have accomplished. The paper is really interesting and should be an important contribution. |