Lee Altenberg's Home Page > Papers | E-mail me

Resolvent Positive Linear Operators Exhibit the Reduction Phenomenon

Lee Altenberg

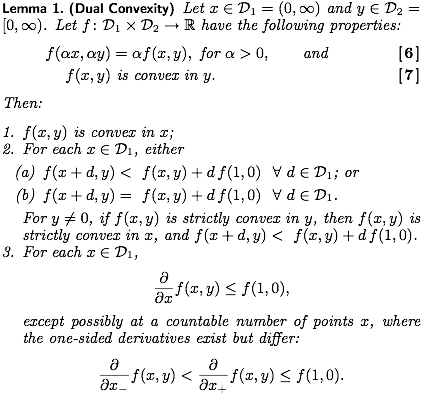
2012, Proceedings of the National Academy of Sciences, 109 (10): 3705-3710.

Abstract

The spectral bound, s(α A + β V), of a combination of a resolvent positive linear operator A and an operator of multiplication V, was shown by Kato to be convex in β ∈ ℜ. This is shown here to imply, through an elementary lemma, that s(α A + β V) is also convex in α > 0, and notably, ∂ s(α A + b V) / ∂ α ≤ s(A ). Diffusions typically have s(A) ≤ 0, so that for diffusions with spatially heterogeneous growth or decay rates, greater mixing reduces growth. Models of the evolution of dispersal in particular have found this result when A is a Laplacian or second-order elliptic operator, or a nonlocal diffusion operator, implying selection for reduced dispersal. These cases are included under the general result here and shown to be part of a single, broadly general, `reduction' phenomenon.

Reviews

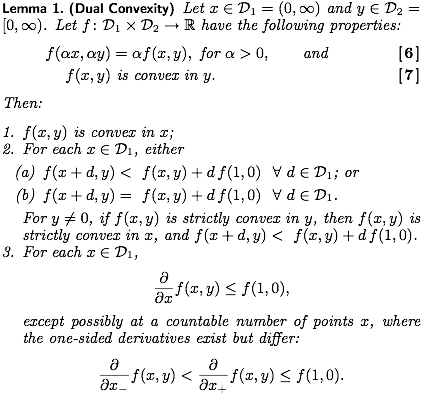
The 2012 PNAS paper by the PI was an exceptionally important result in mathematical population biology.

— Anonymous National Science Foundation panelist

I thoroughly enjoyed reading this short gem of a paper. ... . It is superbly elegant as a piece of mathematics and a true example of perspicacity.

— Anonymous PNAS reviewer

Because the paper achieves conceptual unification and significant generalization for an important set of ideas in modeling the ecological and evolutionary aspects of dispersal, and does so by introducing some elegant and significant new mathematics, I think it makes an important contribution to science.

— Anonymous PNAS reviewer