Lee Altenberg's Home Page >
Papers |
E-mail me
Fundamental Properties of the Evolution of Mutational Robustness
Lee Altenberg
2015, arXiv preprint arXiv:1508.07866
Abstract
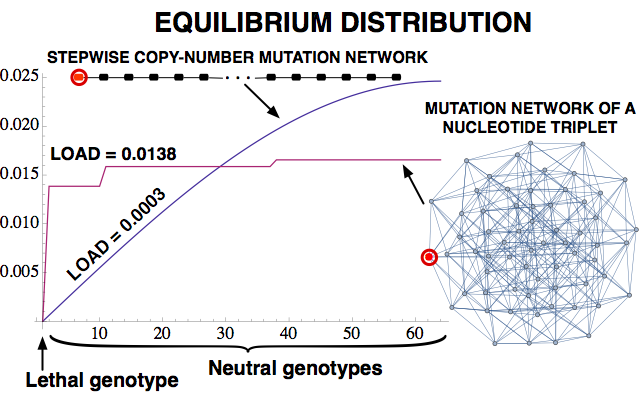
Evolution on neutral networks of genotypes has been found in models to concentrate on genotypes with high mutational robustness, to a degree determined by the topology of the network. Here analysis is generalized beyond neutral networks to arbitrary selection and parent-offspring transmission. In this larger realm, geometric features determine mutational robustness: the alignment of fitness with the orthogonalized eigenvectors of the mutation matrix weighted by their eigenvalues. "House of cards" mutation is found to preclude the evolution of mutational robustness. Genetic load is shown to increase with increasing mutation in arbitrary single and multiple locus fitness landscapes. The rate of decrease in population fitness can never grow as mutation rates get higher, showing that "error catastrophes" for genotype frequencies never cause precipitous losses of population fitness. The "inclusive inheritance" approach taken here naturally extends these results to a new concept of dispersal robustness.

