Lee Altenberg's Home Page >
Papers |
E-mail me
Open Problems in the Spectral Analysis of Evolutionary Dynamics
Lee Altenberg
Pages 73-102 in Frontiers of Evolutionary Computation, ed. Anil Menon. Series: Genetic Algorithms And Evolutionary
Computation Series, Vol. 11, Kluwer Academic Publishers, Boston, MA, 2004.
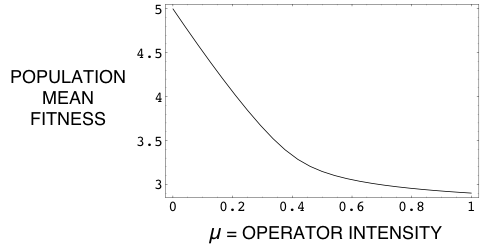
Karlin's Theorem on operator intensity.
Abstract
For broad classes of selection and genetic operators, the dynamics of evolution can be completely characterized by the spectra of the operators that define the dynamics, in both infinite and finite populations. These classes include generalized mutation, frequency-independent selection, uniparental inheritance. Several open questions exist regarding these spectra:
- For a given fitness function, what genetic operators and operator intensities are optimal for finding the fittest genotype? The concept of rapid first hitting time, an analog of Sinclair's "rapidly mixing" Markov chains, is examined.
- What is the relationship between the spectra of deterministic infinite population models, and the spectra of the Markov processes derived from them in the case of finite populations?
- Karlin proved a fundamental relationship between selection, rates of transformation under genetic operators, and the consequent asymptotic mean fitness of the population. Developed to analyze the stability of polymorphisms in subdivided populations, the theorem has been applied to unify the reduction principle for self-adaptation, and has other applications as well. Many other problems could be solved if it were generalized to account for the interaction of different genetic operators. Can Karlin's theorem on operator intensity be extended to account for mixed genetic operators?

