


Next: The ``NK'' Adaptive Landscape
Up: Evolving Better Representations through
Previous: Introduction
The method of evolving representations is to expand the genome one gene at a time by randomly altering the genotype-phenotype map function to include one additional argument. If that alteration reduces fitness, it is rejected, and another attempt made until an alteration that increases fitness is found. Once this is done, a conventional GA is run with this expanded genome to adapt it to a new fitness peak. Then, another round of genome expansion is run. This is illustrated in Figure 1.
Figure:
The genome growth algorithm using constructional selection to evolve the representation.
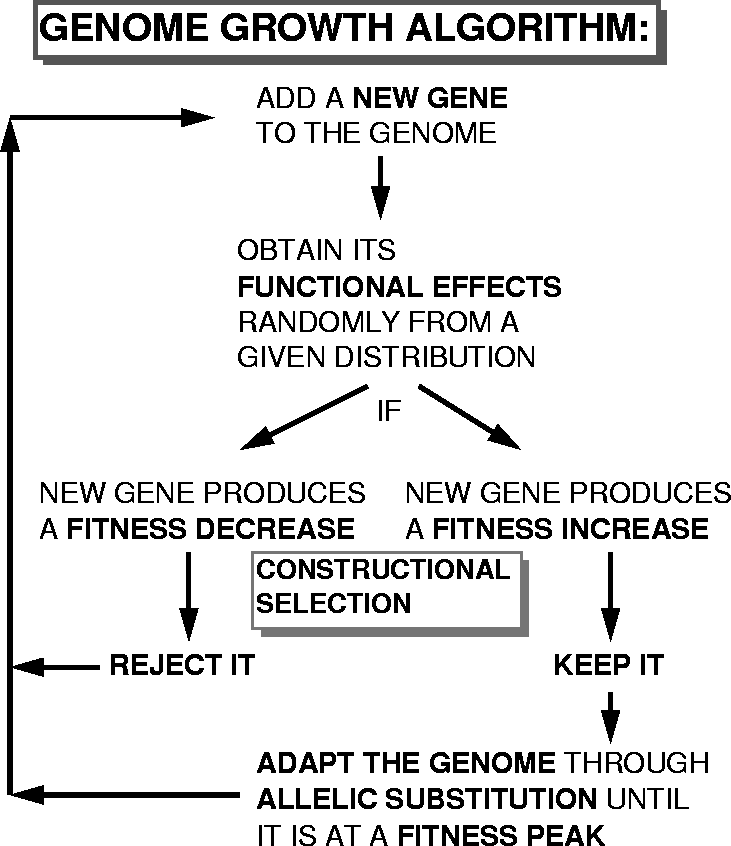 |
This method is expressed formally as follows. Let there be n genes in the genome. The allelic value, xi, for each gene i is an element of the gene's own domain space, Gi (for binary coding,
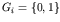 ;
for real valued GAs,
;
for real valued GAs, 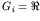 ;
in genetic programming, Gi could be the function or terminal sets or both). A genotype is an array,
;
in genetic programming, Gi could be the function or terminal sets or both). A genotype is an array,
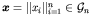 ,
of the allelic values, where
,
of the allelic values, where
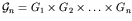 is the genotype space (in typical GAs, the domain spaces Gi are identical).
is the genotype space (in typical GAs, the domain spaces Gi are identical).
A genotype-phenotype map function,
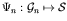 ,
maps the genotype
,
maps the genotype
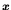 to the search space
to the search space 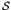 .
A fitness function w(s) is defined on each point
.
A fitness function w(s) is defined on each point
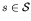 in the search space.
in the search space.
As the genome grows, one obtains a sequence of maps:
When a new gene is added to the genome, the genotype-phenotype map is modified from 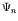 to
to
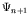 .
The modification is made by a probabilistic operator with probabilities
.
The modification is made by a probabilistic operator with probabilities
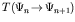 .
It is here that heuristic knowledge of the search space must be incorporated by the designer, since random search through the space of all possible genotype-phenotype maps is no better than random search through
.
It is here that heuristic knowledge of the search space must be incorporated by the designer, since random search through the space of all possible genotype-phenotype maps is no better than random search through 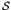 .
One must have an a priori expectation that some of the modifications will produce new maps that are only incrementally changed from old maps (as in [3]). This allows one to relocate the problem of knowledge incorporation to a level where it may be more naturally accommodated.
.
One must have an a priori expectation that some of the modifications will produce new maps that are only incrementally changed from old maps (as in [3]). This allows one to relocate the problem of knowledge incorporation to a level where it may be more naturally accommodated.
For example, this would be the case with series representation
![$s = \Psi_n(\mbox{\boldmath\(x\)\unboldmath }) = \sum_{i=1}^n [a_i\cos(\omega_i) + b_i\sin(\omega_i)]$](img26.gif) ,
where
,
where
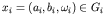 .
Another example is a genetic programming approach, where new functions and terminals can be appended to the parse tree [7].
.
Another example is a genetic programming approach, where new functions and terminals can be appended to the parse tree [7].
Let us return to the idea that an evolved point in the search space has some aspects that are highly adapted, and others that are not yet adapted. If this partition into sub-goals is possible (and for some search spaces it may not be), then one would like to augment the genotype-phenotype map in a way that leaves the highly adapted traits unaffected while exploring the unadapted traits. Yet these ``traits'' (e.g. subgoals) are usually not directly observable, but are abstract, emergent properties of the fitness function. If one has a priori reason to believe that at least some of the modifications
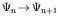 will be able to correctly partition the adapted traits from the unadapted ones, then constructional selection is a means by which to incorporate those modifications into the genotype-phenotype map. This can be illustrated in a model of genome growth using Kauffman's ``NK'' adaptive landscape model.
will be able to correctly partition the adapted traits from the unadapted ones, then constructional selection is a means by which to incorporate those modifications into the genotype-phenotype map. This can be illustrated in a model of genome growth using Kauffman's ``NK'' adaptive landscape model.



Next: The ``NK'' Adaptive Landscape
Up: Evolving Better Representations through
Previous: Introduction
Lee Altenberg
1998-05-27

![]() ,
maps the genotype
,
maps the genotype
![]() to the search space
to the search space ![]() .
A fitness function w(s) is defined on each point
.
A fitness function w(s) is defined on each point
![]() in the search space.
in the search space.
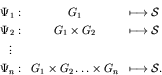
![]() ,
where
,
where
![]() .
Another example is a genetic programming approach, where new functions and terminals can be appended to the parse tree [7].
.
Another example is a genetic programming approach, where new functions and terminals can be appended to the parse tree [7].
![]() will be able to correctly partition the adapted traits from the unadapted ones, then constructional selection is a means by which to incorporate those modifications into the genotype-phenotype map. This can be illustrated in a model of genome growth using Kauffman's ``NK'' adaptive landscape model.
will be able to correctly partition the adapted traits from the unadapted ones, then constructional selection is a means by which to incorporate those modifications into the genotype-phenotype map. This can be illustrated in a model of genome growth using Kauffman's ``NK'' adaptive landscape model.