Non-Generic Properties of Evolved Landscapes

Existing theory for adaptive walks on NK landscapes [11,8,12,13] is derived for generic landscapes, i.e. landscapes that one would typically obtain from a random sampling of landscapes with given values of n and k. The applicability of these results to biological examples assumes that evolutionary processes produce such generic adaptive landscapes. However, the distribution of fitness peaks in the NK landscapes grown here under constructional selection are nowhere near the distributions for generic NK landscapes with identical genotype-phenotype maps.

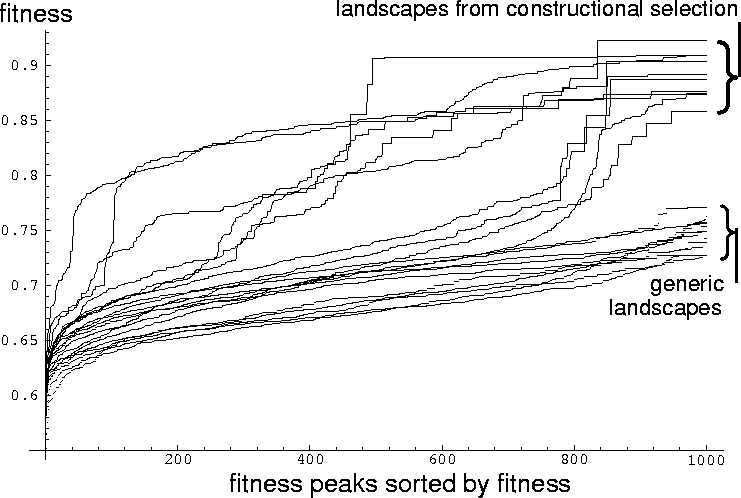
Constructional selection produces genotype-phenotype maps that are much more finely tuned to the fitness function under which they evolved. To illustrate this, the distribution of fitness peaks for several landscapes evolved under constructional selection are plotted in figure 8. For comparison, distributions are plotted for landscapes using the same genotype-phenotype map, but with fitness functions, $\Phi$, chosen a priori. Each point represents the fitness peak obtained by starting an adaptive walk from a randomly sampled genotype. The distributions are plotted by sorting the fitness peaks by size (the transpose of the figure therefore represents the cumulative probability distribution for fitness peaks). The width of horizontal plateaus represents the size of the domain of attraction for a particular fitness peak.

  

Figure: Distributions of fitness peaks of NK landscapes: upper 10 plots are for adaptive landscapes evolved under selection; lower 10 plots are with the same type-phenotype maps but randomized fitness functions. In each plot, the peaks attained from 1000 random starting genotypes are sorted by fitness. Plateaus indicate large domains of attraction for the peak.

The plateaus, and discontinuities between them, indicate fewer and larger domains of attraction for the evolved landscapes, i.e. they are smoother than the generic landscapes. The distributions for the generic landscapes follow roughly the Gaussian approximation derived by Weinberger [13]. While the least fit peaks are approximately the same for both evolved and generic landscapes, at various points in the ranking, the fitness of the evolved landscapes grows much higher. Interestingly, the jumps in the distribution are highly variable.

An additional beneficial outcome of constructional selection is that the genotypes resulting at the end of the run are usually the apparent global fitness peak. In 77% of adaptive landscapes evolved under constructional selection (304 sampled), the genotypes attained at the end of genome growth were fitter than any other adaptive peak found (from 250 other starting genotypes). Of the remaining landscapes, only 19% of the peaks arrived at from random initial genotypes were fitter than the genotype attained at the end of genome growth.